Persamaan
Diferensial Biasa (PDB) adalah persamaan yang melibatkan satu atau lebih
turunan fungsi satu peubah. Solusi dari PDB adalah fungsi tertentu yang
memenuhi persamaan tersebut.
Dengan
c adalah sembarang konstanta yang tidak diketahui. Sehingga solusi PDB
di atas disebut juga solusi umum. Solusi khusus bisa diperoleh bila ada lagi
sebuah persamaan yang merupakan syarat batasnya.
Secara umum, dapat
ditulis:
sehingga diperoleh
Walaupun
ada banyak metode Untuk mencari solusi analitik dari persamaan Diferensial
Biasa (PDB), tetapi pada umumnya terbatas pada PDB yang spesifik. Pada
kenyataan-nya banyak PDB yang tidak dapat dicari solusi analitiknya tetapi
solusi numeriknya dapat diperoleh. Walaupun
solusi analitik dapat diperoleh tetapi rumit, biasanya lebih dipilih solusi
numeriknya.
PDB dan PDS
Persamaan diferensial
dapat dibedakan menjadi dua macam tergantung pada jumlah variabel bebas.
Apabila persamaan tersebut mengandung hanya satu variabel bebas, persamaan
disebut dengan persamaan diferensial parsial (PDP) atau biasa disebut PDS
(persamaan differensial sebagian). Derajat (order) dari persamaan ditentukan oleh
derajat tertinggi dari turunannya.
Contoh PDB dan PDS
- PDB berorder satu, karena turunan tertingginya adalah turunan pertama.
- PDB berorder dua mengandung turunan kedua sebagai turunan tertingginya, seperti bentuk di bawah ini:
- Contoh persamaan diferensial parsial dengan variabel bebas x dan t adalah:
- Misalkan suatu persamaan diferensial biasa berorder satu, sebagai berikut:
- Penyelesaian dari persamaan tersebut adalah:
- yang memberikan banyak fungsi untuk berbagai nilai koefisien C. Gambar 8.1, menunjukkan beberapa kemungkinan dari penyelesaian persamaan (8.2), yang tergantung pada nilai C.
- Untuk mendapatkan penyelesaian tunggal diperlukan informasi tambahan, misalnya nilai y(x) dan atau turunannya pada nilai x tertentu. Untuk persamaan order n biasanya diperlukan n kondisi untuk mendapatkan penyelesaian tunggal y(x)
- Apabila semua n kondisi diberikan pada nilai x yang sama (misalnya x0), maka permasalahan disebut dengan problem nilai awal. Apabila dilibatkan lebih dari satu nilai x, permasalahan disebut dengan problem nilai batas. Misalnya persamaan (8.1), disertai kondisi awal yaitu x = 0, nilai y = 1 atau:
- Substitusikan persamaan (8.3) ke dalam persamaan (8.2) memberikan:
- Dengan demikian penyelesaian tunggal yang memenuhi persamaan:
- Penyelesaian persamaan (8.1) dan persamaan (8.3) adalah mencari nilai y sebagai fungsi dari x. Persamaan diferensial memberikan kemiringan kurva pada setiap titik sebagai fungsi x dan y. Hitungan dimulai dari nilai awal yang diketahui, misalnya di titik (x0, y0).
- Kemudian dihitung kemiringan kurve (garis singgung) di titik tersebut. Berdasar nilai y0 di titik x0 dan kemiringan fungsi di titik-titik tersebut dapat dihitung nilai y1 di titik x1 yang berjarak Δx dari x0. Selanjutnya titik (x1, y1) yang telah diperoleh tersebut digunakan untuk menghitung nilai y2 di titik x2 yang berjarak Δx dari x1.
- Prosedur hitungan tersebut diulangi lagi untuk mendapatkan nilai y selanjutnya, seperti pada Gambar 8.2.
Metode Euler
Metode Euler adalah
salah satu dari metode satu langkah yang paling sederhana. Di banding dengan
beberapa metode lainnya, metode ini paling kurang teliti. Namun demikian metode
ini perlu dipelajari mengingat kesederhanaannya dan mudah pemahamannya sehingga
memudahkan dalam mempelajari metode lain yang lebih teliti.
Metode Taylor
Metode Euler dapat diturunkan dari Deret
Taylor: Metode ini pada dasarnya adalah
merepresentasikan solusinya dengan beberapa suku deret Taylor. Misalkan solusi
dari persamaan diferensial tersebut dapat ditulis dalam bentuk deret Taylor:
•
Bila hanya sampai suku dibawah ini pada Deret Taylor, maka dinamakan metode Deret Taylor orde-n .
Bila hanya sampai suku dibawah ini pada Deret Taylor, maka dinamakan metode Deret Taylor orde-n .
- Metode Deret Taylor orde-1 disebut metode Euler. Untuk mencari solusi numerik dari PDB:
- sepanjang selang [a, b ], dua suku pertama pada deret Taylor yaitu:
- Sehingga dapat ditulis
yang dapat digunakan mulai t = a sampai ke t = b dengan n -langkah yang panjang langkahnya h = (b − a) /n .
• Contoh: Tentukan x (2) dengan menggunakan Metode Euler (n = 4) untuk persamaan diferensial
bila diketahui syarat awal x (1) = − 4
Penyelesaian
Untuk memperoleh hampiran yang lebih akurat, dapat digunakan Metode Deret Taylor orde yang lebih tinggi. Perhatikan persamaan diferensial berikut ini:
Bila PD tersebut diturunkan beberapa kali terhadap t , diperoleh:
sehingga dapat diperoleh:
Selesaikan persamaan di bawah ini:
Dari x = 0 sampai x = 4 dengan panjang langkah Dx = 0,5 dan Δx = 0,25.
Contoh Metode Euler
Contoh Metode Euler
A. Penyelesaian:
Penyelesaian eksak dari persamaan diatas adalah:
Penyelesaian numerik dilakukan secara bertahap pada beberapa titik yang berurutan. Dengan menggunakan persamaan (8.6), dihitung nilai yi + 1 yang berjarak Δsx = 0,5 dari titik awal yaitu x = 0. Untuk i = 0 maka persamaan (8.6), menjadi:
B. Penyelesaian:
Dari kondisi awal, pada x = 0 nilai fungsi y(0)= 1, sehingga:
Kemiringan garis di titik (x0 ; y0) adalah:
sehingga:
C. Penyelesaian:
Nilai eksak pada titik x = 0,5 adalah:
Jadi kesalahan dengan metode Euler adalah:
2.5 RUNGE-KUTTA
Penggunaan metode Taylor memerlukan penurunan fungsi f (t, y ) secara analitik. Berikut akan diperkenalkan metode untuk menghasilkan y i dengan akurasi yang sama seperti metode Taylor tanpa melakukan penurunan terhadap fungsi f (t, y ). Metode yang paling sederhana adalah metod Runge Kutta orde 2 .
Runge Kutta Orde 2
Perhatikan deret Taylor untuk y (t + h ) sebagai berikut:
Bentuk y’(t ) dan y’’(t ) diubah menjadi bentuk f (t, y ) dan turunan - turunan parsialnya.
Perhatikan bahwa
Dengan menggunakan aturan rantai untuk fungsi dua peubah persamaan dan mensubsti-tusikan persamaan (9.1) ke bentuk berikut diperoleh
Sehingga deret Taylor untuk y (t + h ) dapat diubah menjadi sebagai berikut
Perhatikan metode Runge - Kutta orde 2 yang menggunakan kombinasi linear 2 fungsi untuk menyatakan y (t + h ) :
Dengan
Kita perlu mencari nilai - nilai A, B , P , Q sehingga persamaan (9.2) akurat. Ekspansi Taylor untuk fungsi dua peubah f 1 sebagai berikut.
Substitusikan persamaan ini ke persamaan (9.2) diperoleh persamaan untuk y (t + h )
sehingga diperoleh persamaan - persamaan berikut
Solusi yang sesuai dengan keadaan ini adalah
Secara umum, metode Runge - Kutta orde 2 adalah sebagai berikut
dengan
Runge Kutta Orde 4
Dengan cara yang sama, diperoleh metode Runge-Kutta orde 4 sebagai berikut
dengan
Diketahui PDB
dy/dx = x + y ; y(0) = 1
hitung y(0.10) dengan metode Heun (h = 0.02)
penyelesaian:
dietahui:
f(x,y) = x + y
a = x0 = 0
b = 0.10
h = 0.02
maka n = (0.10 - 0)/0.02 = 5 (jumlah langkah)
langkah-langjah:
x1 = 0,02 y(0)1 = y0 + hf(x0, y0)
= 1 + 0.02(0+1)
= 1.0200
Y(1)1 = y0 + (h/2)[f(x0,y0)+f(x1,y(0)1)]
= 1 + (0.02/2)(0+1+0.02+1.0200)
= 1.0204
X2 = 0.04 y(0)2 = y1 + hf(x1, y1)
= 1.0204 + 0.02(0.02 + 1.0204)
= 1.0412
Y(1)2 = y1 + (h/2)[f(x1, y1) + f(x2, y(0)2)]
= 1.0204 + (0.02/2)[0.02 + 1.0204 + 0.04 + 1.0412]
=1.0416
…
X5 = 0.10 y(0)5 = y4 + hf(x4, y4)
Y(0)5 = y4 + (h/2)[f(x4, y4) + f(x5,y(0)5)]
= 1.1104
Jadi, y(0.10) 1.1104
Program dengan Menggunakan SCILAB
OUTPUT
TUGAS REKAYASA KOMPUTASIONAL
PERSAMAAN DIFERENSIAL BIASA
NAMA KELOMPOK :
1. DESI SPECTRYANI (51411884)
2. GALUH SEKAR AMBAR SARI (50408955)
3. MUMHANA ARTANTI (55411034)
KELAS : 3IA24
DOSEN : ARY BIMA KURNIAWAN, ST., MT.
sumber : http://bima.staff.gunadarma.ac.id/Downloads/folder/0.14



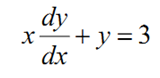




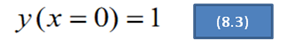














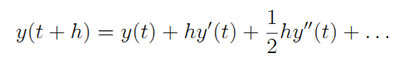









gmn ya caranya aku bisa mempelajari sendiri biar tidak pusing heheheee
ReplyDeleteThis comment has been removed by the author.
ReplyDeleteini di pointernya apaan lagi ganggu banget
ReplyDelete